客服QQ號：2992009682
返回因為懸索橋的主體結(jié)構(gòu)做到了沒有彎矩，只承受拉力。這幾乎是效率最高的結(jié)構(gòu)體系。
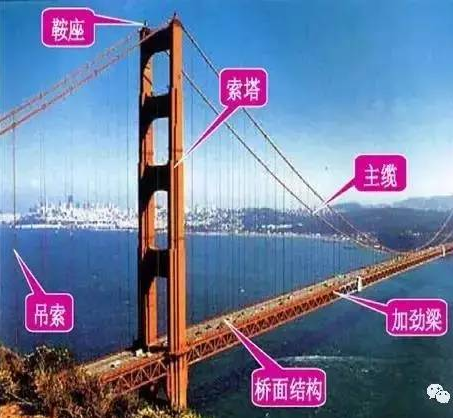
簡 單說，拿筷子做類比。隨便一用力就可以把筷子掰斷，這就是筷子在受彎；但幾乎很少有人能夠把筷子拉斷，這就是筷子在受拉。幾乎所有的材料，受拉的效能都要 遠遠高于受彎的效能。（具體的分析，可以參照這個回答：為什么對木棍，鐵棒等，折斷比拉斷更容易）再舉個例子，想想一下晾衣服。受彎的例子就是晾衣桿，木 頭的、竹子的、金屬的，這些桿子都要有足夠的直徑，否則很容易就被衣服壓斷了；受拉的例子則是晾衣繩，很細(xì)的一根繩子，所用的材料比木桿子少得多，晾上衣 服之后下垂的弧度很大，但一般情況下很難被拉斷。與軸心拉壓相比，受彎是一個效率極低的承載方式。一定程度上，提高結(jié)構(gòu)效能就是盡量的把受彎轉(zhuǎn)化為受拉或 者受壓。如果同時能夠做到盡量減輕結(jié)構(gòu)自重，那就更完美了。拱結(jié)構(gòu)就是轉(zhuǎn)化為受壓的例子，而懸索橋則是轉(zhuǎn)化為受拉的例子。
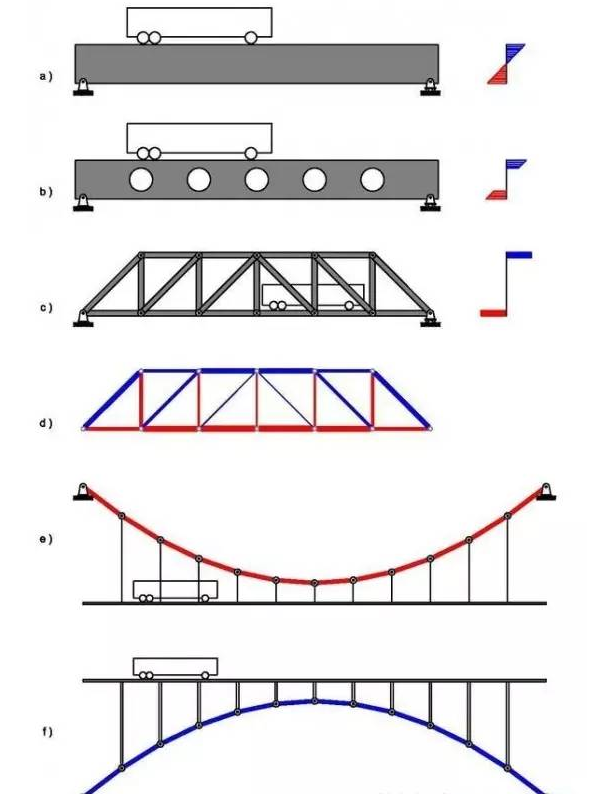
a 圖就是最普通的梁式橋，完全依靠受彎承載。這種形式非常常見，地鐵、高架、小型公路橋梁，幾乎全部是這樣的。右邊是它的截面的應(yīng)力分布，上下表面大，中間 位置幾乎為零。也就是說，整個截面的應(yīng)力并不是平均分配的，而是存在一個“水桶效應(yīng)”，盡管中間位置幾乎沒有應(yīng)力，但是，只要上下邊緣達到了極限，整個截 面就離破壞不遠了。上下邊緣處的應(yīng)力就是這個水桶最短的那塊木板。
既然中間截面幾乎為零，那么為什么不把它們省略呢？于是，就有了b 圖這種開孔梁。截面中間部位應(yīng)力很小的那些地方被省去，減輕了自重。拉壓應(yīng)力集中在上下邊緣處。
把 這個趨勢進一步擴大，也就是把原來的梁式結(jié)構(gòu)進一步格構(gòu)化，去掉應(yīng)力小的部位，保留最基本的部位，我們就得到了 c 圖的這種桁架結(jié)構(gòu)。d 圖是它的大致內(nèi)力分布，紅色受拉，藍色受壓。它的截面分布更加合理，上弦桿件受壓，下弦桿件受拉，中間沒用的部位全是空的。著名的南京長江大橋就是這樣的 結(jié)構(gòu)形式。
如 果把這個最優(yōu)化的趨勢做到極致，那就達到了 e 圖這種的懸索結(jié)構(gòu)。整個懸索承受同樣大小的拉力，整個懸索的拉力由支座處的錨固平衡。其實這種結(jié)構(gòu)非常好理解，把 e 圖想象成一根晾衣繩，上面晾了11件衣服，而晾衣繩的兩端，需要牢固的栓在墻上或者柱子上。很容易理解吧？
f 圖所示的拱橋就是另一個方向的極致，與 e 圖上下對稱，f 圖中的拱結(jié)構(gòu)只承受壓力，也不承受彎矩。但與純受拉的懸索結(jié)構(gòu)相比，受壓的拱結(jié)構(gòu)還牽扯到穩(wěn)定問題。舉個例子，你用腳踩放在地上的空易拉罐，很難把它踩 碎，但是很容易就把它踩變形、踩扁了。因此，拱結(jié)構(gòu)的效率還是比不上懸索結(jié)構(gòu)。
那為什么懸索非得是這種形狀呢？也很好理解，弄一根鐵鏈，或者自行車鏈條，兩端固定，中間自由下垂，得到的就是上面 e 圖的這個形狀。自由繩索在自重作用下自由下垂所形成的曲線，一般稱為懸鏈線。觀察一下蜘蛛網(wǎng)，它們就是近似的懸鏈線。
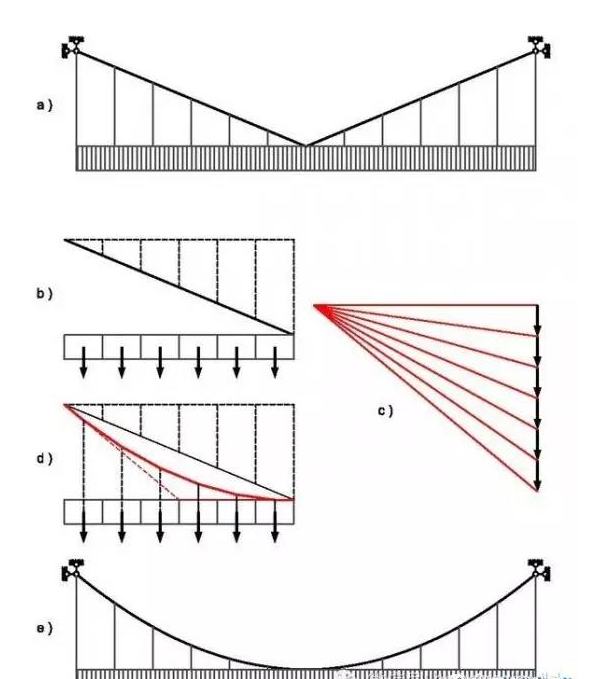
假 設(shè)承受均布荷載的懸索，最初始的形狀是 a 圖這種倒三角形。因為是對稱結(jié)構(gòu)，所以取它的一半進行分析。如 b 圖所示，類似微積分的概念，近似把這一半均勻分為6份，每份荷載相同。c 圖是這種情況下的力多邊形，而 d 圖中的紅色折線就是這一組力的索多邊形。以這條紅色折線為幾何構(gòu)形，我們得到 e 圖所示的懸索。因為考慮的是均布荷載，所以不需要再二次迭代了，再迭代一次的結(jié)果只會是同樣的這條紅色折線。因此，紅色折線就是均布荷載下的最優(yōu)懸索，不 承受彎矩，只承受拉力。注意，這個不是懸鏈線，而是一條拋物線，因為它承受的是均布荷載，而不是自重。
關(guān) 于懸鏈線的數(shù)學(xué)認(rèn)知，說起來也很有代表性，人類對于知識的認(rèn)知就是這樣的漸進式的過程。亞里士多德認(rèn)為拋出物體的運動軌跡是先直線，然后再下落。伽利略 意識到亞里士多德錯了，得出了正確的拋物線的表達式，但是，伽利略錯誤的認(rèn)為一條懸鏈自然下垂，得到的也是一條拋物線。隨后，容吉烏斯指出，在受水平向均 布荷載的情況下，懸鏈的形狀才是拋物線，也就是我們上面 e 圖的情況。由于懸鏈的自重是沿曲線方向分布的，水平方向的荷載分量并不均布，所以自然懸鏈不是拋物線。雖然容吉烏斯指出了伽利略的錯誤，但他沒能找到正確 的答案。直到1691年的一次數(shù)學(xué)競賽中，萊布尼茨、惠更斯和約翰·伯努利才各自獨立得出了正確的懸鏈線的數(shù)學(xué)表達形式。
當(dāng) 然，制約懸索橋跨度和安全性能的不僅僅是豎向荷載，還有側(cè)向的抗風(fēng)設(shè)計。1940年，美國塔克馬海峽大橋在風(fēng)中坍塌，引起了工程學(xué)界對抗風(fēng)設(shè)計的重視。 今天的懸索橋，技術(shù)水平已經(jīng)達到了很高的程度。目前最長跨度的懸索橋是日本的明石海峽大橋，主跨1991米。其原設(shè)計為1990米，但1995年的阪神大 地震震中距大橋只有4公里，導(dǎo)致正在建設(shè)中的兩側(cè)橋塔之間的水平距離增加了1米。
從懸索的數(shù)學(xué)推導(dǎo)，到驚人的主跨接近2000米的大橋，這就是一條從簡單理論模型到復(fù)雜實際設(shè)計的道路。數(shù)學(xué)理論和力學(xué)理論如何指導(dǎo)實際的工程設(shè)計，這就是一個很好的例子。而所謂工程師，就是能夠優(yōu)雅簡潔的完成這一過程的人。
橋梁結(jié)構(gòu)形式主要有幾種：
1、簡支梁，2，連續(xù)梁（連續(xù)剛構(gòu)）3，拱橋，4，斜拉橋，5，懸索橋
橋梁除了承擔(dān)車輛荷載外，更重要的是要承擔(dān)自身的自重。
簡支梁的最大跨度是50m，在跨度增長時，為了能夠增強抵抗能力，需要加大梁高，而梁高的增長會增大自重，而且自重產(chǎn)生的效應(yīng)即彎矩，是與跨徑成平方關(guān)系，因此當(dāng)跨度達到一定時，無論怎么提高梁高，都沒法增加跨度了，因為橋梁會被自己的自重壓垮。
跨度繼續(xù)提高，就需要采用連續(xù)梁與連續(xù)剛構(gòu)形式了，這兩種形式會在支座位置產(chǎn)生負(fù)彎矩，減小跨中的正彎矩，改善橋梁的受力。
最 大跨度，大概做到250m。拱橋的跨越能力很好，如專家一所述，拱結(jié)構(gòu)承擔(dān)很大的壓力，會改善其受力性能。但是這是理想情況，即拱橋承受均布荷載的形 式。這種形式荷載的來源通常是自重。所以拱橋的自重對拱橋的受力，經(jīng)常是有利的，而車輛荷載是集中力，集中力會產(chǎn)生彎矩。彎矩太大了之后，拱圈就受不了 了。同時混凝土雖然說抗壓能力很好，但是受壓構(gòu)件有個很致命的穩(wěn)定問題，跨度大了之后，穩(wěn)定問題就會很突出了。
混凝土拱橋，鋼筋混凝土拱橋，目前最大跨度是420米，萬縣長江大橋。而目前正在設(shè)計的，北盤江大橋，跨度達到了445m。
斜 拉橋的跨度可以達到1000m左右，斜拉橋的主要受力構(gòu)件是斜拉索，加勁梁，主塔。在主梁上，每隔一段就設(shè)置一個斜拉索，這相當(dāng)于給加勁梁加了一個彈性 支撐，把大跨度的斜拉橋分成若干個小跨度的加勁梁，這樣加勁梁的受力就不會隨著跨度的增長而成幾何級數(shù)增長。而斜拉索的強度又很高，這樣跨度就做大了。但 是因為斜拉索的角度問題，所以斜拉索會給加勁梁有一個軸心壓力，這個壓力就會引起穩(wěn)定問題，所以1樓說拉壓力比彎矩要好，實際上是不準(zhǔn)確的。
懸 索橋在斜拉橋的基礎(chǔ)上有變化，懸索橋的主要受力構(gòu)件是大纜，錨釘。加勁梁不再是主要受力構(gòu)件了。懸索橋的大纜上垂下吊桿，也將加勁梁分成若干段，只是與 斜拉橋不一樣的是，吊桿與加勁梁垂直。此時，吊桿完全起一個支撐作用，對加勁梁不會產(chǎn)生水平分力，這就避免了加勁梁的穩(wěn)定問題。車輛在加勁梁上運行，車輛 荷載和加勁梁自重，通過吊桿傳遞到大纜上，所有荷載由大纜承擔(dān)，最后傳遞到兩頭的錨錠上。加勁梁就類似與小跨度的簡支梁，這時候不控制受力了。斜拉橋和懸 索橋跨度很大的原因，就是用斜拉索和吊桿，將大跨度的加勁梁分割成了若干個彈性支撐的小跨度橋。使得跨度的增長不會大幅度的增加自重。
同時專家一提出的：受壓是不是一定比受彎更好，恐怕值得商榷
懸索橋之所以要轉(zhuǎn)換為拉力，是與材料有密切關(guān)系的。因為我們只能得到抗拉的高強材料，鋼絞線的抗拉強度1869MPa，而一般形成梁的鋼材Q345，屈服強度是345MPa，有5倍的差距。如果也有像斜拉索的高強板材，其他橋型的跨度也能做大。
拱橋也是利用類似的原理，混凝土材料與圬工材料抗壓性能很好，所以我們轉(zhuǎn)化為壓力。我們轉(zhuǎn)化為什么力，是根據(jù)材料性能選擇的，而不是因為拉壓比彎曲好。
舉一個例子，如果一個能夠有非常高強度的中長柱，一個受純彎，一個受軸壓，誰更容易破壞呢？再取到極限狀態(tài)，如果強度無窮高，又是什么情況呢？恐怕軸壓的穩(wěn)定問題會更突出吧。
另外專家一舉的筷子容易彎斷不容易拉斷的例子，來說明抗彎比較困難。實際上，不容易拉斷的生活經(jīng)驗，是因為無法提供足夠的拉力。要想施加足夠的拉力，必須要保證手和筷子有足夠的摩擦力，這是很難做到的。如果用拉力機加載，是可以加到筷子纖維的抗拉強度。
無論是受拉還是受壓，還是受彎，最后都是反映到應(yīng)變或者應(yīng)力上，其本質(zhì)是剪切應(yīng)變能達到極限狀態(tài)。只是因為我們的加載或者試驗方式，實施起來可能有的更容易，有的不那么容易而已。
